Native functions standard library¶
Math¶
math.copy(A,B)¶
Copy the arrayin the array
, element by element:
.
math.fill(A,c)¶
Fill each element of the arraywith the constant
:
.
math.addscalar(A, B, c)¶
Computewhere
is a scalar.
math.add(A, B, C)¶
Computewhere
,
and
are three arrays of the same size.
math.sub(A, B, C)¶
Computewhere
,
and
are three arrays of the same size.
math.mul(A, B, C)¶
Compute
where
,
and
are three arrays of the same size.
Note that this is not a dot product.
math.div(A, B, C)¶
Compute
where
,
and
are three arrays of the same size.
An exception will be triggered if a division by zero occurs.
math.min(A, B, C)¶
Write the minimum of each element ofand
in
where
,
and
are three arrays of the same size:
.
math.max(A, B, C)¶
Write the maximum of each element ofand
in
where
,
and
are three arrays of the same size:
.
math.clamp(A,B,C,D)¶
Clamp each elementand store it in
so that
.
math.dot(r, A, B, n)¶
math.stat(V, min, max, mean)¶
Compute the minimum, the maximum and the mean values of array.
math.argbounds(A, argmin, argmax)¶
Get the indices argmin and argmax corresponding to the minimum respectively maximum values of array.
math.sort(A)¶
Sort the arrayin place.
math.muldiv(A, B, C, D)¶
Compute multiplication-division using internal 32-bit precision:
.
An exception will be triggered if a division by zero occurs.
math.atan2(A, Y, X) [1]¶
Compute
using the signs of
and
to determine the quadrant of the output, where
,
and
are three arrays of the same size.
Note that
and
will produce
.
math.rot2(A, B, angle) [1]¶
Rotate the array
by angle, write the result to
.
Note that
and
must both be arrays of size 2.
math.sqrt(A, B)¶
Computewhere
and
are two arrays of the same size.
math.rand(v)¶
Return a random valuein the range
.
Since a scalar is considered to be an array of size one, you can use these functions on scalars:
var theta = 16384
var cos_theta
call math.cos(cos_theta, theta)
Double-ended queues¶
The Deque native library provides functions for double-ended queue operations in an object-oriented style on specially-formatted arrays.
The array for a deque object must be of size 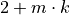 where
where 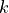 is the size of the tuples [2] in the deque, and
is the size of the tuples [2] in the deque, and 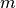 is the maximum number of tuples to be stored.
is the maximum number of tuples to be stored.
An index 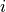 into a deque is between two elements: the integer
into a deque is between two elements: the integer 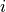 counts the number of elements to the left of the index.
counts the number of elements to the left of the index.
deque.size(Q,n)¶
Set 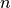 to the number of elements in deque
to the number of elements in deque 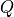 . If
. If 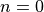 then
then 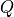 is empty. Note that
is empty. Note that 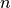 must be divided by the tuple size to obtain the number of tuples in
must be divided by the tuple size to obtain the number of tuples in 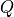 .
.
deque.push_front(Q,A)¶
Insert tuple 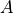 before the first tuple of deque
before the first tuple of deque 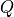 .
.
deque.push_back(Q,A)¶
Insert tuple 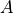 after the last tuple in deque
after the last tuple in deque 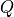 .
.
deque.pop_front(Q,A)¶
Remove the first 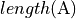 elements of deque
elements of deque 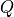 and place them in tuple
and place them in tuple 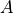 .
<<<<<<< HEAD
.
<<<<<<< HEAD
deque.pop_back(Q,A)¶
Remove the last 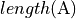 elements of deque
elements of deque 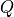 and place them in tuple
and place them in tuple 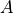 .
.
deque.pop_back(Q,A)¶
Remove the last 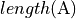 elements of deque
elements of deque 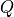 and place them in tuple
and place them in tuple 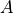 .
.
>>>>>>> nsis
deque.get(Q,A,i)
^^^^^^^^^^^^^^^^^^^^^^^^
Copy into tuple 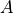 ,
, 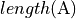 elements from deque
elements from deque 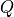 starting from index
starting from index 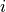 .
.
deque.set(Q,A,i)¶
Copy into deque 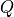 starting at index
starting at index 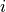 ,
, 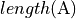 elements from tuple
elements from tuple 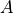 .
.
deque.insert(Q,A,i)¶
Shift right the suffix of deque 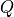 starting at index
starting at index 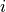 by
by 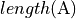 elements, then copy tuple
elements, then copy tuple 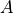 into the deque
into the deque 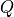 at that index.
at that index.
deque.erase(Q,i,k)¶
Erase 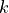 elements from deque
elements from deque 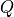 at index
at index 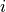 by shifting the suffix starting from
by shifting the suffix starting from 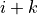 left. Length
left. Length 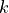 should be the tuple size or a multiple.
should be the tuple size or a multiple.
Example¶
Here is a simple motion queue, that accepts operations defined by a time and motor speeds, and executes them first-in, first-out.
var operation[3] # Tuple of size 3
var Queue[2 + (3*40)] # Store up to 40 operation tuples
var n
sub motion_add
call deque.push_back(Queue, event.args[0:2])
onevent timer0
call deque.size(Queue, n)
if n > 0 then
call deque.pop_front(Queue, operation)
timer.period[0] = operation[0]
motor.left.target = operation[1]
motor.right.target = operation[2]
end
| [1] | (1, 2, 3, 4) The trigonometric functions map the angles 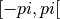 radians to radians to 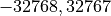 .
The resultant sin and cos values are similarly mapped, namely .
The resultant sin and cos values are similarly mapped, namely 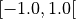 to to 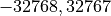 . . |
| [2] | A tuple is simply a small array of values that are inserted in the deque together |
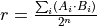
 where
where 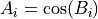 where
where